1. Tujuan
1. Dapat membandingkan antara frekuensi-frekuensi harapan dengan frekuensi-frekuensi teramati.
2. Dapat mengetahui data sebuah sampel yang diambil menunjang hipotesis yang menyatakan bahwa populasi asal sampel tersebut mengikuti suatu distribusi yang telah ditetapkan.
3. Dapat melatih kemampuan mahasiswa/mahasiswi untuk mengatasi masalah industri yang berhubungan dengan chi-square.
4. Dapat mengembangkan keterampilan mahasiswa/mahasiswi dalam menggunakan dan menganalisa dengan program SPSS 10.00
2. Landasan Teori
Sebaran chi-square (chi-kuadrat) adalah sebaran yang dimiliki oleh suatu statistik bila ragam contoh acak berukuran n ditarik dari populasi normal dengan ragam s2. Sebaran chi-kuadrat dirumuskan :

· Uji Kebaikan Suai
Uji kebaikan suai adalah uji yang didasarkan pada seberapa baik kesesuaian antara frekuensi yang teramati dalam data contoh dengan frekuensi harapan yang didasarkan pada sebaran yang dihipotesiskan. Untuk menentukan apakah suatu populasi mempunyai sebaran teoritik tertentu. (Wallpole, 1996).
Uji kebaikan suai dirumuskan :

Lambang OI dan ei masing-masing menyatakan frekuensi yang teramati dan frekuensi harapan bagi sel ke-I, sedangkan nilai x2 merupakan sebuah nilai bagi peubah acak x2 yang sebaran penarikan contohnya sangat menghampiri sebaran chi-kuadrat.
Bila frekuensi yang teramati sangat dekat dengan frekuensi harapannya nilai x2 akan kecil. Hal ini menujukkan adanya kesesuaian yang baik, bila frekuensi yang teramati berbeda cukup besar dari frekuensi harapannya nilai x2 akan besar sehingga kesesuaiannya akan buruk. Kesesuaian yang baik akan membawa pada penerimaan Ho, sedangkan kesesuaian yang buruk akan membawa pada penolakan Ho.
Untuk taraf nyata a nilai kritiknya x2 a dapat diperoleh pada tabel. Dengan demikian wilayah kritiknya adalah x2 > x2 a. Kriteria keputusan ini tidak untuk digunakan pada frekuensi harapan yang kurang dari 5. Persyaratan ini mengakibatkan penggabungan sel yang berdekatan sehingga mengakibatkan berkurangnya derajat bebas. Banyaknya derajat bebas dalam uji kebebasan suai yang didasarkan pada sebaran chi-kuadrat adalah sama dengan banyaknya sel dikurangi dengan banyaknya besaran yang diperoleh dari data pengamatan (contoh) yang digunakan dalam perhitunganfrekuensi harapannya.
· Uji Kebebasan Suai
Prosedur uji chi-kuadrat dapat pula digunakan untuk menguji hipotesis kebebasan antara 2 peubah. Uji kebebasan suai dirumuskan :

dengan :
V = (r - 1) (c - 1) derajat bebas
Bila x2 = x2 a tolak hipotesis o bahwa kedua penggolongan itu bebas pada taraf nyata a, bila selainnya terima Ho (Wallpole, 1996).
· Pengujian Beberapa Proporsi
Statistik chi-kuadrat untuk uji kebebasandapat juga diterapkan untuk menguji apakah k populasi binom memiliki parameter yang sama. Uji ini merupakan selisih antara dua proporsi menjadi selisih antara k proporsi. Jadi kita berkepentingan untuk menguji hipotesis Ho=P1-P2=…=Pk.
Lawan alternatifnya bahwa populasi proporsi itu tidak semuanya sama, yang ekuivalen dengan pengujian bahwa terjadinya keberhasilan atau kegagalan tidak tergantung pada populasi yang diambil contohnya. Untuk melakukan uji ini pertama kita harus mengambil contoh acak bebas yang berukuran masing-masing n1, n2 …, nk bentuk tabel kontingensi sama dengan 2 x k.
Frekuensi harapan dihitung seperti cara yang telah diterangkan diatas, kemudian bersama-sama dengan yang teramati dimasukan kedalam rumus untuk uji kebebasan yaitu :

dengan :
V= (2-1) (k-1) derajat bebas
Dengan mengambil wilayah kritik diekor bagian kanan yang berbentuk x2 > x2 a maka Ho dapat disimpulkan.
Perlu diingat bahwa statistik yang kita gunakan sebagai dasar pengambilan keputusan, hanya dihampiri sebaran chi-kuadrat, nilai chi kuadrat hitung bergantung pada frekuensi sel sebaran chi yang kontinue menghampiri sebaran contoh bagi x2 dengan sangat baik, asal V>1.
Dalam tabel kontingensi 2 x 2 dengan 1 derajat bebas, biasanya digunakan koreksi Yate bagi kekontinuan. Rumus yang terkoreksi adalah :

Bila frekuensi harapannya besar, nilai yang terkoreksi maupun yang tidak terkoreksi hampir sama. Bila f harapan antara 5 da 10 koreksi Yate harus diterapkan. Bila f <>
selanjutnya anova satu arah,
ANOVA SATU ARAH
1. Tujuan :
1. Untuk mengetahui dan memahami uji statistik dengan menggunakan ANOVA, terutama ANOVA 1 arah,
2. Untuk mengetahui persoalan dan masalah-masalah yang berkaitan dengan uji ANOVA 1 arah dalam kehidupan sehari-hari.
3. Agar dapat menyelesaikan persoalan uji ANOVA 1 arah dan menarik kesimpulan yang sesuai dengan persoalan yang diujikan..
2. Teori
Analisis ragam (Analysis of Variance) atau yang lebih dikenal dengan istilah ANOVA adalah suatu teknik untuk menguji kesamaan beberapa rata-rata secara sekaligus. Uji yang dipergunakan dalam ANOVA adalah uji F karena dipakai untuk pengujian lebih dan 2 sampel.
Anova dapat digolongkan kedalam beberapa kriteria, yaitu :
1. Klasifikasi 1 arah
ANOVA klasifikasi 1 arah merupakan ANOVA yang didasarkan pada pengamatan 1 kriteria.
2. Klasifikasi 2 arah
ANOVA kiasifikasi 2 arah merupakan ANOVA yang didasarkan pada pengama
tan 2 kritenia.
3. Klasifikasi banyak arah
ANOVA banyak arah merupakan ANOVA yang didasarkan pada pengamatan banyak kriteria.
Pada pembahasan kali ini, dititikberatkan pada pengujian ANOVA 1 arah yaitu pengujian ANOVA yang didasarkan pada pengamatan 1 kriteria. Setiap kriteria dalam pengujian ANOVA mempunyai level.
Contoh :

Gambar Kriteria dan Level
Asumsi pengujian ANOVA :
1. Populasi yang akan diuji berdistribusi normal
2. Varians/ragam dan populasi yang diuji sama
3. Sampel tidak berhubungan satu dengan yang lain
Tujuan dan pengujian ANOVA ini adalah untuk mengetahui apakah ada pengaruh dan berbagai kriteria yang diuji terhadap hasil yang diinginkan. Inisal, seorang manajer produksi menguji apakah ada pengaruh kebisingan yang ditimbulkan oleh mesin-mesin produksi di pabrik pada hasil perakitan sebuah komponen yang cukup kecil dan sehuah sirkuit yang memerlukan konsentrasi yang tinggi dan seorang operator rakit.
Dalam pengujian ANOVA ini, dipergunakan rumus hitung sebagai berikut:

Dimana :

selanjutnya pembahasan tentang anova dua arah,
ANOVA DUA ARAH
1. Tujuan :
1. Untuk mengetahui dan memahami uji statistik dengan menggunakan ANOVA, terutama ANOVA 2 arah,
2. Untuk mengetahui persoalan dan masalah-masalah yang berkaitan dengan uji ANOVA 2 arah dalam kehidupan sehari-hari.
3. Agar dapat menyelesaikan persoalan uji ANOVA 2 arah dan menarik kesimpulan yang sesuai dengan persoalan yang diujikan.
2. Teori
Analisis ragam (Analysis of Variance) atau yang lebih dikenal dengan istilah ANOVA adalah suatu teknik untuk menguji kesamaan beberapa rata-rata secara sekaligus. Uji yang dipergunakan dalam ANOVA adalah uji F karena dipakai untuk pengujian lebih dari 2 sampel.
Anova dapat digolongkan kedalam beberapa kritenia, yaitu :
1. Klasifikasi 1 arah
ANOVA kiasifikasi 1 arah merupakan ANOVA yang didasarkan pada pengamatan 1 kriteria.
2. Klasifikasi 2 arah
ANOVA klasifikasi 2 arah merupakan ANOVA yang didasarkan pada pengamatan 2 kriteria.
3. Klasifikasi banyak arah
ANOVA banyak arah merupakan ANOVA yang didasarkan pada pengamatan banyak kriteria.
Pada pembahasan. kali ini, dititikberatkan pada pengujian ANOVA
2 arah yaitu pengujian ANOVA yang didasarkan pada pengamatan 2 kriteria. Setiap kriteria dalam pengujian ANOVA mempunyal level.
Contoh :
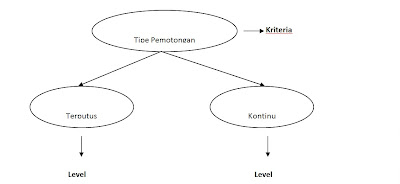
Gambar Kriteria dan Level
Asumsi pengujian ANOVA:
1. Populasi yang akan diuji berdistribusi normal
2. Varians/ragam dan populasi yang diuji sama
3. Sampel tidak berhubungan satu dengan yang lain
Tujuan dan pengujian ANOVA 2 arah ini adalah untuk mengetahui apakah ada pengaruh dan berbagai kriteria yang diuji terhadap hasil yang diinginkan. Misal, seorang manajer teknik menguji apakah ada pengaruh antara jenis pelumas yang dipergunakan pada roda pendorong dengan kecepatan roda pendorong terhadap hasil penganyaman sebuah karung plastik pada mesin circular.
Dalam pengujian ANOVA ini, dipergunakan rumus hitung sebagai berikut:
Tabel Analisis Ragam Klasifikasi Dua Arah

Sumber: Walpole, Ronald E. (1995)
Dimana:

materi diatas dapat di download di
sini


Posting Komentar